LAB 07A - COMPUTATIONAL INTEGRATION

Task

Create a program which calculates the percentage of people within a user defined height range.

Your task for this exercise is to write a program which calculates the percentage of finding someone, chosen at random, who has a height within some user defined range. For instance, the final output of your program will look similar to:



In order to accomplish this task, you are given a mathematical equation that you need to implement as a C++ function. This function will take a height parameter, compute the result of the provided equation using the input height, and then return the result of that computation. Within your main function, you then need to perform a computational integration, which pretty much amounts to a simple Riemann sum (remember week 1 from calculus!?!). More info on Riemann sums at the end of this lab description.

Height Distribution:

For this lab assignment, we assume that human heights can be estimated using a normalized normal (aka Gaussian or bell-curve) distribution. Specifically, we assume that the human heights distribution has an average of 65 inches (5 foot 5 inches) and a standard deviation of 3 inches. This distribution looks like



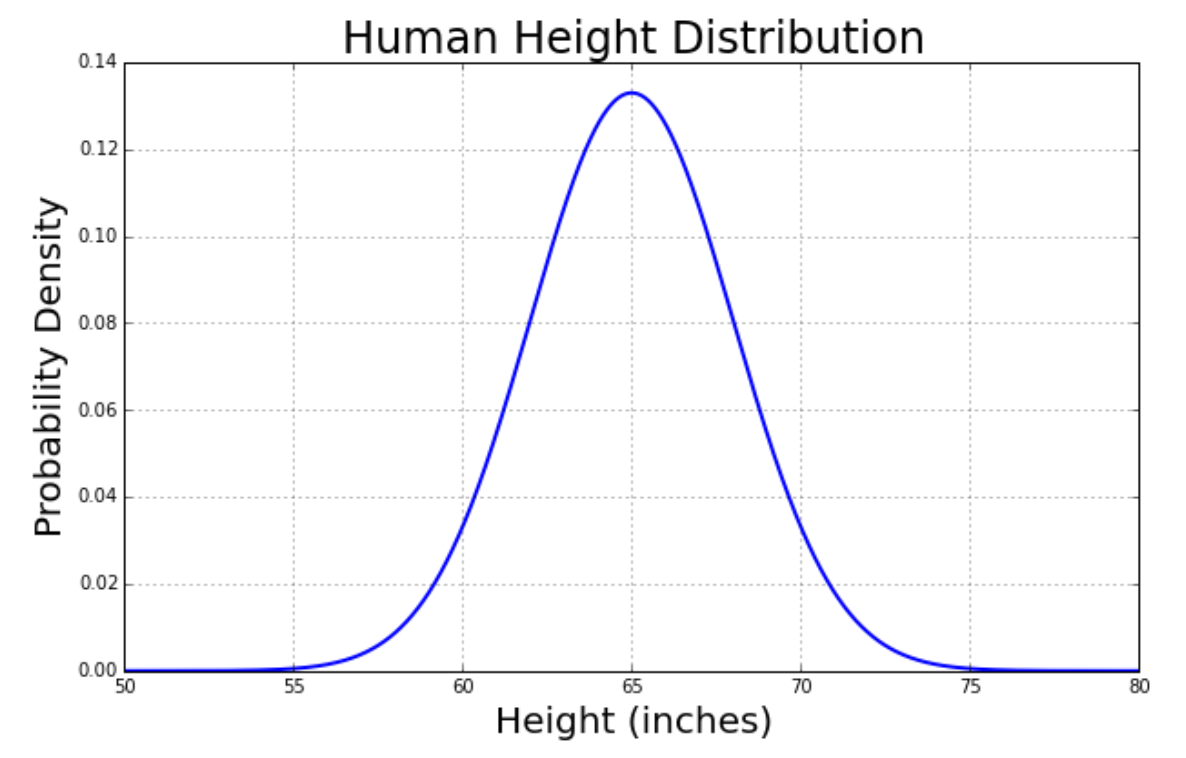
which is represented by the equation:



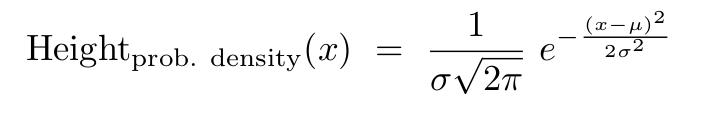
where x represents any height, μ represents the mean of the distribution (i.e., 65 inches), and σ represents the standard deviation (i.e., 3 inches).

This equation is an example of a probability density; thus, when it is integrated within a certain range, the result of that integration represents the probability of finding the input argument (height, in this case) within that range.

A direct integration of this type of function gives a value between 0 and 1, where 0 corresponds to 0% and 1 corresponds to 100%. In the special case where the integration range extends from negative infinity to positive infinity, which is just a fancy way of saying “what is the probability of finding somebody with ANY height”, then the result of this integration should return 100% (or, more specifically, 1). This is the meaning of the term normalized.

Computational Integrations

A computational integration accomplishes the same task as the mathematical integrations you learned in your calculus classes; in this case, however, we're letting the computer do the work for us. Sweet!

You may be thinking: "So what's the point of learning to do this the hard way?!?" Well! A mathematical integration can be performed both implicitly:



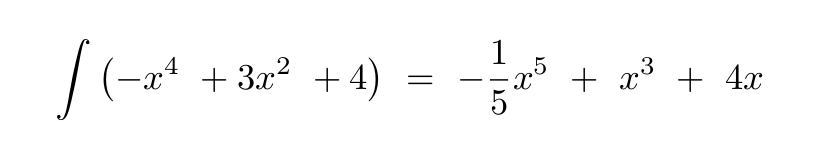
or explicitly:



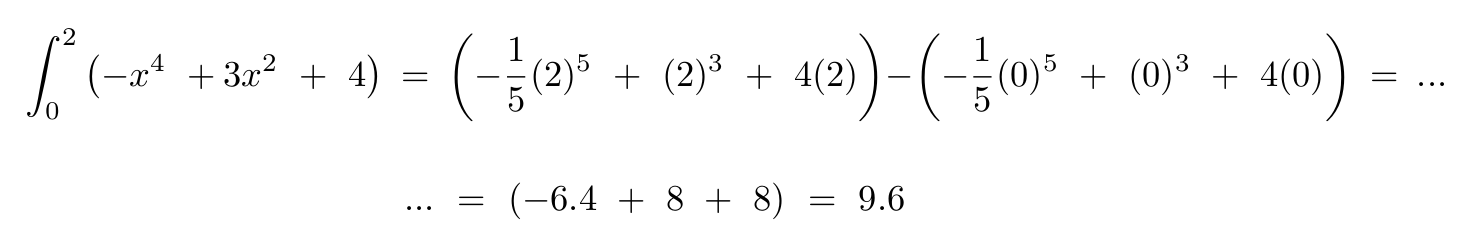
Generally speaking, a computer can only perform an integration explicitly; in other words, the whole equation must be redone every time you wish to change the range of your integration. Implicit integrations are certainly preferable, when they can be performed; alas, the real world is not as friendly as calculus would have you believe! Most equations that you are exposed to as engineers and scientist are not simple; thus, integrating them may prove to be exceedingly difficult or (perhaps) down-right impossible. In fact, the Gaussian distribution of human heights in this lab is an example of one of these 'impossible to integrate' functions. Go ahead and look up these types of functions on an integration table, and you will see that the answer involves something called the error function ( erf() ), which is a stand in for some very complex mathematics that are far beyond the scope of this lab. In any case, as far as you are concerned at this time, using a computational integration ends up being the only reliable way to integrate our height distribution. On the bright side, computational integrations are surprisingly simple! In fact, you likely learned how to do them in the first few weeks of your MATH 111 class (via calculating a Riemann Sum).

Riemann Sum

A Riemann Sum is a technique used to estimate the area underneath a curve. The process follows these steps:

1. Start with an equation that you want to integrate. For our case, we'll use the human heights equation above.
2. Decide on a range you want to integrate within. Let's choose 0 to 2.
3. Divide this range into N equal segments. Let's use 4.
4. Find the height of the equation at the left of each segment, which gives you 4 rectangular strips.
5. Sum the area of each strip to estimate the area under the curve.

The result would look something like (for a different distribution):



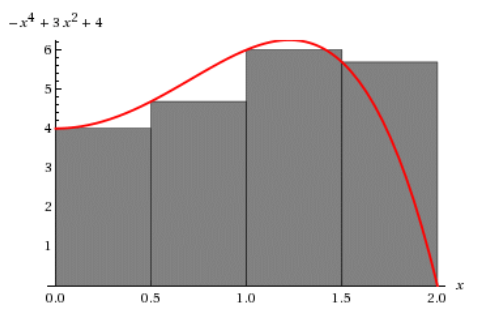
Although this process gets us in the ballpark of the real answer (i.e., the result from our explicit integration), it is clearly not perfect. What if we use 8 segments:



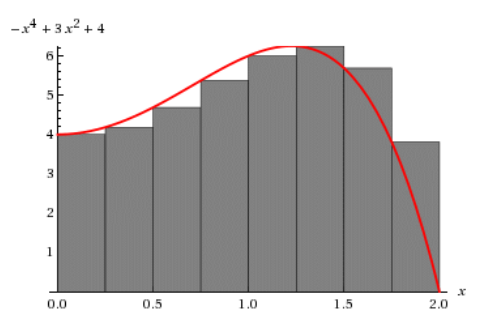
Or 20 segments:



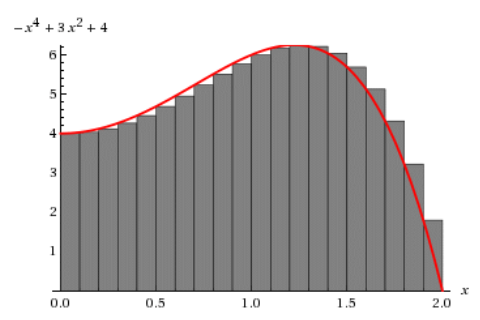
As a general rule, the more segments you use, the closer you get to the real answer. And, since computer programming allows us to let a computer do the work, there's no reason why we don't use a large number of segments, e.g., 100!



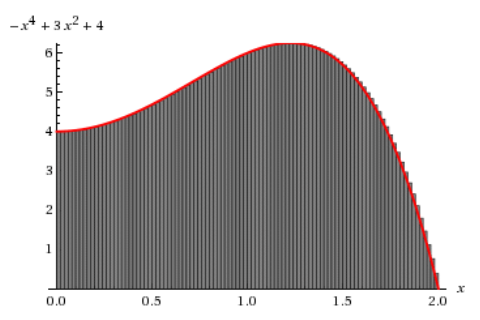
Of course, no matter how many segments we use, we will never get exactly the right answer. But we can get close enough.

If you would like to play around with Riemann Sums, check out Wolfram's Riemann Sum Calculator.

Or, as an alternative, write a solution for this lab that uses the Riemann Sum technique to estimate the area under our human heights curve. Begin the program asking the user to enter the range to integrate within and the number of segments to use in the computational integration. See the Task section of this lab above to remind yourself of the C++ function you need to write. This lab will be submitted with Homework 7.